Dynamic Programming

  * Matrix Chain Multiplication(행렬 체인 곱) 

 

 

 

 

-행렬 곱 문제를 해결하는 알고리즘

-괄호 묶는 방법의 수 세기

 

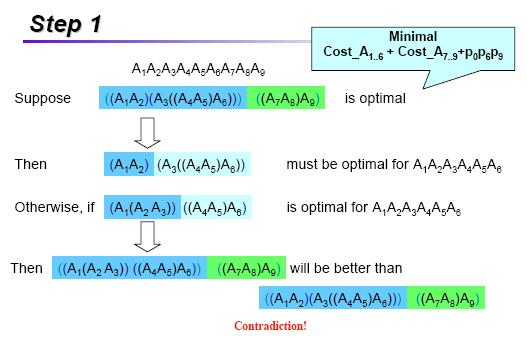
Step 1 : The Struct of an Optimal Parenthesization ( 최적 괄호 묶기의 구조)

            최적 부분 구조를 찾은 뒤, 부분 문제에 대한 최적해를 그 문제에 대한 최적해를 구성하는  

            데 사용.

           -A[i]A[i+1]......A[j]의 곱 A[i...j] 를 계산할 경우,(A[i] 는 행렬), 이들의 괄호 묶는 방법의

           결과는 어떤 정수 k(i<=k<j)에 대해 A[k]와 A[k+1] 사이에서 나누어 져야 함

           -즉, 어떤 값 k에 대해 먼저 A[i...k] 와 A[k+1...j]를 계산한 후, 최종의 결과 A[i..j]를 얻기

           위해 그 둘을 곱한다

           -괄호 묶기의 비용은 행렬 A[i..k]와 A[k+1..j]를 계산하는데 드는 비용, 그리고 그 둘을 곱

           하는데 드는 비용의 합이 된다.      

 

 

 

Step 2 : Recursive Solution (재귀적 해)

           -최적해의 비용을 부분 문제에 대한 최적해에 의해 재귀적으로 정의

           -m[i][j] : 행렬 A[i...j]를 계산하는데 필요한 최소한의 스칼라 곱의 수

 

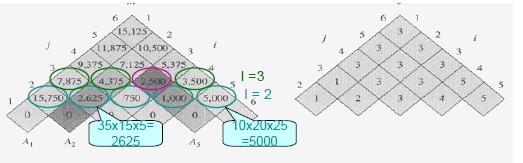
Step 3 : Compute the Optimal Cost (최적 비용 계산)

           -점화식의 해를 재귀적으로 구하는것 대신, 동적 프로그래밍 알고리즘 개발의 세번째 단계

           를 수행하고, 상향식 접근 방법과 테이블을 사용하여 최적의 비용계산

 

 

 

 

   

Step 4. 최적해 구성

           -Matrix-Chain-Order에 의해 계산된 테이블 s와 인덱스 i,j를 바탕으로 최적 괄호 묶는 방법

           을 출력

 

 

*참고 자료 : Introduction to Algorithms, 알고리즘 수업 강의자료